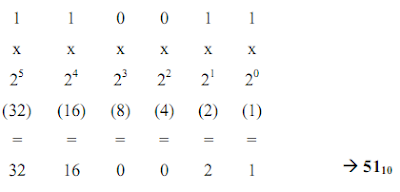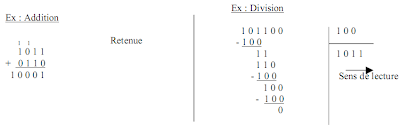Les Systèmes de numération
1) Introduction
L‘homme a besoin d‘un système de codage pour identifier, quantifier, qualifier les objets, les lieux, les Évènements… Ces codes lui permettent de mémoriser, traiter et communiquer les informations. Ils peuvent être :
- le langage
- l‘écriture
- le graphisme
- la gestuelle
- …
- Une liste de symboles prédéfinis : l'alphabet
- Des règles d‘utilisation des symboles :
* Plusieurs mots => phrase
- des règles de syntaxe pour ordonner les mots dans une phrase
Pourquoi ?
- Raison technologique : il est simple de représenter en électronique un phénomène à 2 états.
Le courant passe => 1
Le courant ne passe pas => 0
Même si avez l‘impression du contraire en utilisant certains logiciels ⁄ l‘ordinateur ne comprend que les 0 et les 1. Cette logique est appelée le langage binaire.
2) Le langage binaire
- Le binaire possède un alphabet simplifié à deux symboles : 0 et 1
- Sa base de numération est donc 2 (2 symboles).
- Normalisation d‘écriture : n2 (par exemple 1012)
Un nombre en base 10, tel que nous l‘employons d‘habitude, devrai être noté sous la forme n10, par exemple : (135)10
Un peu de vocabulaire : - Chaque élément binaire pouvant prendre la valeur 0 ou 1 est appelé un digit binaire (Binary digit)
- Une suite de 4 bits est appelée quartet
- Une suite de 8 bits est appelée octet.
Depuis 12/98, l‘organisme international IEC (International Electrotechnical Commission), a définit les mesures suivantes :
1Ko = 1000 octets (210 bits)
1M o = 1000 Ko = 1000 x 1000 octets
1Go = 1000 M o = 1000 x 1000 x 1000 octets
1To = 1000 Go = 1000 x 1000 x 1000 x 1000 octets
Mais de nombreux logiciels, parfois même certains systèmes d‘exploitation, utilisent toujours la notation Antérieure à 1998 pour laquelle 1Ko = 1024 octets (210 bits)
Attention en anglais, octet se traduit par byte. Il faut donc absolument éviter la confusion entre bit et byte.
Donc 1 Ko = 1KB (Notez l'utilisation d'un B majuscule pour différencier Byte et bit)
3) Conversions binaires
3.1 Décimal => binaire par division successive :
On divise le nombre en base 10 par 2, puis on divise successivement le quotient de chaque division par 2 jusqu'à ne plus pouvoir diviser par 2. Le nombre binaire s‘obtient en relevant le reste de chaque division en partant de la dernière division vers la première (sens de lecture vers le haut).
Ex : (230)10 à convertir en base 2
Le résultat est donc : (230)10 => (11100110)2
3.2 Décimal => binaire par soustraction
Cette méthode consiste à retrancher du nombre la plus grande puissance de 2 possibles, et ainsi de suite Dans l‘ordre décroissant des puissances. Si on peut retirer la puissance de 2 concernée, on note (1) sinon on note (0) et on contenue de la même manière jusqu'à la plus petite puissance de 2 possible (20 pour les entiers).
Ex : (230)10 à convertir en base 2
Le résultat est donc : (230)10 => (11100110)2
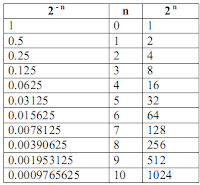
Cette technique implique de connaîre les valeurs décimales associées aux puissances de 2 :
3.3 Conversion binaire => décimal
On multiplie chaque bit par le chiffre 2 élevé à une puissance, croissant par pas de 1, comptée à partir de Zéro en partant de la droit puis on effectue la somme des résultats obtenus.
Soit (110011)2 à convertir en décimal :
3.4 Notion de Poids binaire
Le poids binaire ou « poids du bit » est la puissance à laquelle est élevé le bit lors de la conversion binaire => décimal.
Ainsi, les bits situés à droite du nombre sont les bits de poids faible (leur puissance évolue à partir de zéro). Les bits situés à gauche sont les bits de poids fort (leur puissance est la plus élevée et va en décroissant).
Sur un octet, le bit situé à gauche est le bit de poids fort (27) le plus significatif ou MSB (Most Significant Bit)
alors que le bit le plus à droite (20) est le bit de poids faible ou LSB (Least Significant Bit).
3.5 Exercices de conversion
- 12710 = 111 11112
- 10 01102 = 3810
- 25510 = 1111 11112
- 25610 = 1 0000 00002
- 0010 10102 = 4210
- 1000 00002= 12810
- 3410 = 10 00102
- 1100 01202 = Impossible en base 2
- Quel est le plus petit nombre que peut contenir un octet ?
- Quel est le plus grand nombre que peut contenir un octet (en décimal et en binaire) ?
De la même façon qu'en base 10, il est possible d'effectuer des opérations (addition, soustraction, multiplication et division) directement en binaire suivant les mêmes principes.
3.7 Les nombres fractionnaires
- La partie entière d‘un nombre se traduit en mettant en œuvre des puissances positives de 2.
- Sa parte décimale se traduit en mettant en Œuvre des puissances négatives de 2.
Le nombre binaire obtenu se présente sous la forme d‘une parte entière située à gauche du point "décimal" (ou de la virgule), et d‘une parte fractionnaire située à droite.
Ex. 100.012 est équivalent à 4.2510
3.7.1 La conversion Décimal => Binaire
Il suffit de multiplier par 2, la parte entière ainsi obtenue représentant le poids binaire (1 ou 0). La partie fractionnaire restante est à nouveau multipliée par 2 et ainsi de suite jusqu'à ce qu‘il n'y ait plus de parte fractionnaire ou que la précision obtenue soit jugée suffisante.
Soit 0.62510
Soit 0.62510
Quand il ne reste plus de parte fractionnaire, on s‘arrête. Ainsi 0.62510 devient 0.1012
Tableau des puissances de 2
Tableau des puissances de 2
3.7.2 La conversion Binaire => Décimal
Le principe est similaire :
- On utilise les puissances de 2 négatives en commençant à 2-1
- On parcourt les bits de la gauche vers la droite.
Ex : Convertir 0.1012 en base 10
3.7.3 Exercices de conversion de nombres fractionnaires
4) Le langage hexadécimal
Le langage binaire s‘il est compréhensible par la machine (et peut être appelé à ce niveau langage machine) est Difficilement « assimilable » par l‘homme dès lors qu‘il est questions de grandes séries binaires. On utilise donc un autre système de notation, le système hexadécimal - base 16.
En notation hexadécimale, on utilise un alphabet comportant 16 symboles :
4.1 Conversions décimal - hexadécimal
Décimal => Hexa
On passe d‘un nombre en base 10 à un nombre en base 16 par divisions successives. On note les restes des divisions successives puis on lit ces restes en « remontant ».
Ex : convertir en base 16 le nombre 728 en base 10
donc 72810 = 2D816
Même principe que dans la conversion binaire, mais cette fois, il s‘agit des puissances de 16.
Ex : 13D16 à convertir en base 10
4.2 Passage direct binaire / hexadécimal
Si l'on représente les 16 symboles de l‘alphabet hexadécimal en binaire, on constate que l‘on utilise pour chacun d‘eux un maximum de 4 bit
donc passer du binaire à l‘hexadécimal en décomposant le nombre binaire en bloc de 4 bit en partant de la droite (bits dits de poids faible) et en restituant sa valeur hexadécimale à chacun de ces blocs.
Exemple : conversion de 73210
Le passage de l‘hexadécimal en binaire peut donc se faire de la manière inverse, c'est-à-dire en convertissant les chiffres qui composent le nombre hexadécimal en leur équivalant binaire.
Ainsi 10C16 => (0001 0000 1100)2
Telechargement des fichier:
Pour telecharger ce document clicki ici: http://www.4shared.com/file/vBibUlRUce/COUR-Les_Systmes_de_Numration.html